大学受験の数学で無双する計算力の身につけ方

今回は、計算力を身につけるメリットと、大学受験の数学で無双するための計算力の身につけ方を紹介します。理系専門塾の塾長がレベル別で計算力を上げる方法について解説しますので、数学が苦手な人から得意な人まで是非参考にしてみて下さい!
【この記事を読むべき人】
- 計算ミスが多くて困っている人
- 計算力が低くて大学受験の問題を解くのに苦労している人
- 計算スピードが遅くて共通テストに対応できない人
- 計算力の身につけ方が分からない人
【自己紹介】
百瀬 浩市
「理系のための大学受験塾SoRa」代表。数学の指導において、幅広いレベルの生徒を担当。定期テストで赤点が続いていた生徒が80点を安定して取れるまでに引き上げる、数学が苦手な難関大学志望者を合格点まで導くといった指導実績を持つ。
計算力を身につけた方が良い2つの理由
高校数学の膨大な演習量をこなせないから
素早く正確に計算できる力を持っていないと、高校数学では十分な演習を積むことが出来ません。
高校数学は中学数学と比べて、入試や定期テストで高得点を取るのに必要な演習量は段違いに多いです。私の感覚としては、高校数学では中学数学の6倍もの分量があると考えています(高校数学は数ⅠAⅡBⅢCの6分野からなるので、ムラはあるにしても各分野がそれぞれ中学数学の分量に値するイメージです)
1問1問の習熟度を上げるためには当然何回も問題を解かなければなりません。ただ、あまりに分量が多いために、ほとんどの高校生は十分な演習量を積めないままテストを受けています。
もちろん、そもそもの勉強時間が足りないケースも多いですが、受験生などでは勉強時間を確保できるようになると、計算力がないが故に1問1問に時間がかかって演習量を積めない場合が出てきます。
大学受験でも計算力で差がつくから
大学受験の問題は難しい思考力を問われるイメージがあるかもしれませんが、実際には計算が大変な問題も多いです。そのため、解き方がわかっていても計算ミスで点数を落とす受験生が毎年たくさんいます。
せっかく解法を理解していても、単純な計算ミスで点を失ったり、計算に時間がかかって解ききれなかったりするのは非常にもったいないですよね。
私自身、受験生のときに第一志望校の数学の試験で、大問1の最終問題の式変形で単純な足し算(8+5程度)を間違えた経験があります。しかも、3回も検算したにもかかわらず、3回とも同じミスを繰り返してしまいました。
試験が終わってから間違いに気づいたときの記憶は今でも鮮明に覚えています笑
正確かつ迅速に計算できるようにならなければ、解き方が分かっていたとしても、点数にならないのです。
【レベル別】大学受験の数学で無双する計算力の身につけ方
ここからは、大学受験の数学で無双する計算力を身につける方法を学習者の学力レベルに応じて紹介していきます。レベル別に紹介していますが、レベル1または2から始めるのがおススメです。自分の状況に合わせたところから始めていきましょう。
レベル1:小学算数・中学数学の計算を素早く正確に行う練習
レベル1は、「小学校や中学校の頃から算数や数学が苦手で、内容も忘れている箇所がありそう…」と感じている人向けの内容です。小学算数や中学数学の内容に自信がある人は、次のレベル2から読み進めてOKです。
ただ、小学算数・中学数学だからといって舐めないでください!
これまでの経験上、出来ていると思っている人の半分くらいは、実は完ぺきでなかったりします。小学算数や中学数学の計算問題をやってみると意外と解けないなんてことがよくあるのです。
当たり前のことですが、高校数学は小学算数や中学数学の基礎の上に成り立っています。そのため、小学算数や中学数学の計算がスムーズにできないと、高校数学の内容に入る前につまづいてしまいます。すべての内容を完璧に理解しておいてほしいですが、高校数学と関連して特にスムーズにできないとまずい分野を挙げます。
- 最大公約数・最小公倍数
- 分数の四則演算
- 文字式の四則演算
- 平方根の簡略化(√48=4√3のような計算)
- 因数分解
- 解の公式の運用
これらの計算がスムーズにできる自信がない人は、以下の2冊の参考書を使って演習していくのがおススメです。
小河式プリント中学数学基礎篇 改訂新版 (未来を切り開く学力シリーズ)
小1~小6までで習う内容の演習をすることができます。簡潔な説明と演習用の問題があるので、忘れている部分を思い出しながら取り組むことができます。
中学数学発展篇 方程式と関数 改訂新版 (未来を切り開く学力シリーズ)
上記の小川式プリントシリーズの続きです。中1~中3までの基本的な内容を学ぶことができます。さまざまなパターンの計算問題がたくさん載っているのでドリル的に使うことができます。
使い方としては、上記の二冊を少しずつでよいので毎日やっていきましょう。最初から解くのではなく、自分が苦手としている分野から取り組むので構いません。
ドリルとして解いていきながら、慣れてきたらタイムアタック方式で目標タイムを決めて計算スピードを上げていきましょう。
レベル2:計算を簡略化できるテクニックを学ぶ
レベル1の内容(中学数学以前の計算)はスムーズにできる前提の上で、計算を簡略化するテクニックを学んでいきましょう。
計算を簡略化できると計算量が減るので、自ずと時短になって計算ミスも少なくなります。それに伴って演習がスラスラ進むようになるので、数学の演習量が確保できるようになったり、受験でもミスが減って失点しにくくなったりするなどメリットしかありません。
とはいえ、計算テクニックと一言でいってもなかなかイメージしにくいと思いますので、まずは、問題例を出しながら具体的にどういったテクニックがあるかを紹介していきます。
例1)49、55、52、48の平均を求めよ
この問題をそのまま計算をしようとすると、以下のようになります。
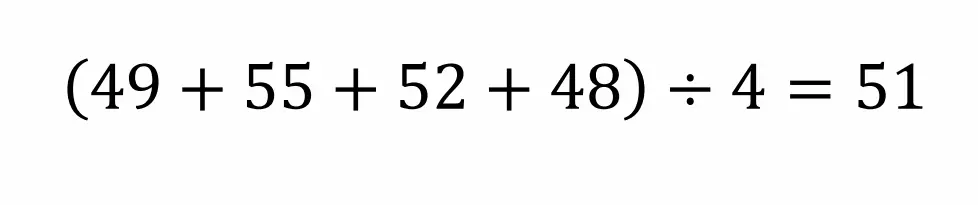
ただ、このやり方だと足し算をするのが大変でミスも発生しそうです。そこで以下のように、50付近の数字を足していることに注目して、各数字と50との差の平均をとって最後に50を足すと速く計算できます。
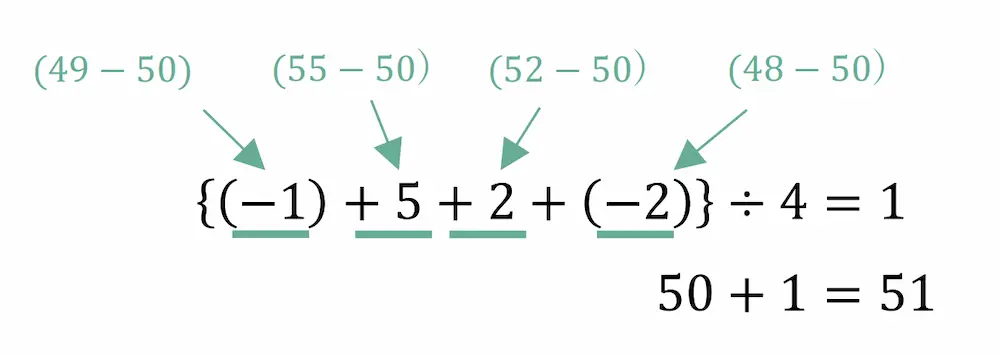
こうすることで、足し合わせる数字が小さくなるので、計算ミスがおきにくくなり、素早く計算できるようになります。
例2)
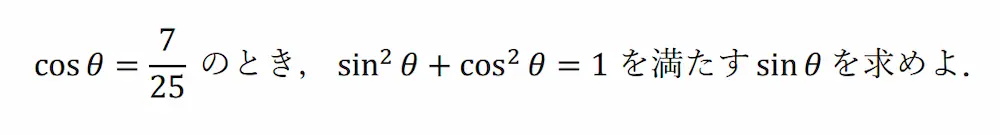
この問題も何も考えずに計算すると↓のようになります。

おそらく、そのまま計算した人は、576の平方根が分からずに、そこでストップするか、素因数分解に時間がかかると思います。
しかし、↓のように最終的に√を取るので、二乗をあえて計算せずに残しておき、因数分解の公式を使うことで簡単に計算することができます。
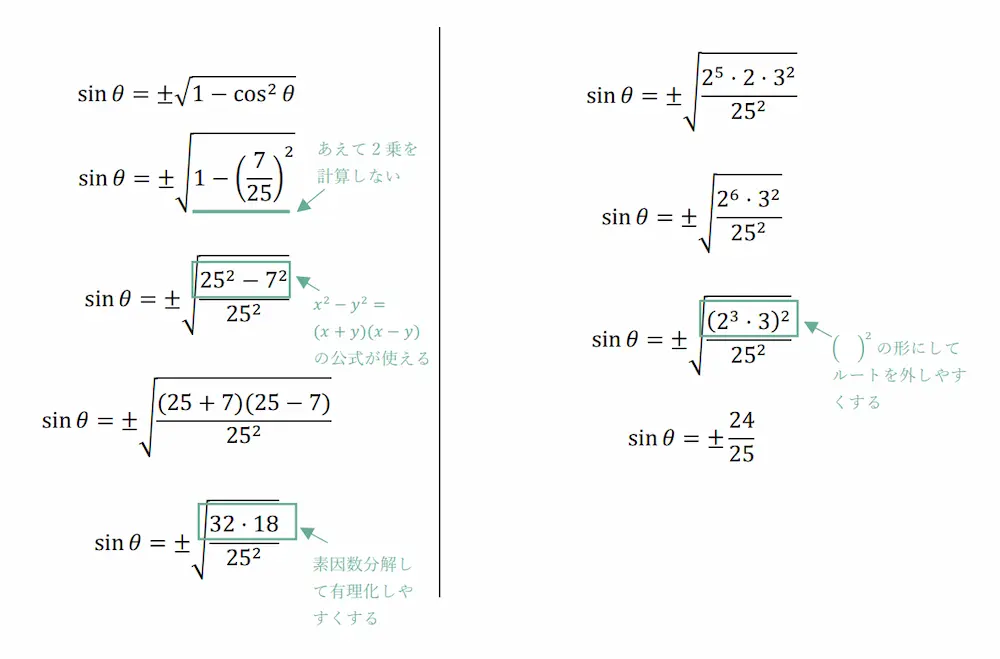
今回紹介したのは、ほんの一例にすぎません。これらのテクニックを身につけるには、どういったテクニックがあって、どういうときに使えるかを学ぶ必要があります。こういった計算テクニックを独学するには、「合格る計算数ⅠAⅡB」がおすすめです。
普通の参考書では省略されているような、計算テクニックを学ぶことができます。特に数学ができる人が、計算の行間でどのように考えているかを学べます。
この参考書についても、いろんな分野の計算が載っているので、まずは自分がやりたいと思う分野から毎日少しずつやっていくのがおすすめです。
レベル3:問題演習を通じて計算力を高める
レベル2で計算を短縮できるテクニックを学んだら、あとはそれを実践の場で活かせるように数学の問題演習を通じて慣れていく必要があります。
演習に使う教材は学校の授業や提出用のワーク、塾の授業や宿題など分野や内容は問いません。大事なのは、獲物を狙うハイエナのように計算を短縮できないかを常に狙いながら計算をしていくことです。
いくら計算のテクニックを学んでも、それを使えなければ意味がありません。計算のテクニックをうまく使えない人は、なんとなく脳死で与えられた式をただ計算しがちです。そうではなく、ちょっと面倒だなと感じた時に「何か抜け道はないのか?」という視点で考える姿勢を持たなければなりません。
もちろん、全ての計算で簡略化できるテクニックが使えるわけではありませんが、そういった心構えで実際に問題を解いていくことが大事になります。
また、ある程度慣れてきたら、自分で制限時間を決めてタイムアタック形式で計算スピードと正確性を上げる訓練をするのもおすすめです。
「このプリントを1枚10分で解く」というように時間制限を課すことで、どのように簡略化できるかを判断するスピードを上げることができます。まだ計算がおぼつかなかったり、その分野の内容が頭に入っていない場合は、無理してやる必要はありませんが、慣れてきたら、そういったトレーニングは非常に有効です。
レベル4:計算ミスノートを作る
最後は受験生や定期テスト前の高校生におすすめの方法です。それは、計算ミスノートを作って自分のミスのクセを分析することです。
ある程度演習量を積んでくると、計算ミスのデータが溜まってきます。それを見返して、どういう時にどういったミスをしているのかを振り返ってみましょう。
もちろん、間違えた時に自分がどこで間違えたのかを見直している前提ですが、どういったときにどういう計算ミスをしているのかを分析することで、自分がよくやるミスのパターンが見えてきます。
例えば、私の場合、「ー(○ー□)」という計算で、□の符号をプラスにしなきゃと注目しすぎるあまり、隣の○をプラスのまま書いてしまうミスをよくやります。
受験生なら過去問に取り組み始めたくらい、定期テスト直前の高校生なら問題集を2周以上した段階で、これまで解いた問題のノートを見返してどういったミスがあるのかを「計算ミスノート」と称して別のノートに記録をつけておきましょう。
このノートを試験直前に見返して、自分がどういったミスをよくするのかを振り返ることで、試験前に意識して気をつけることができます。
もちろん、そういった計算ミスは気をつけていても100%はなくなりませんが、正答率を70%から80%に上げることはできます。特に入試の場合に、合格最低点付近では1点差で多くの受験生がひしめき合うので、1つのミスがあるかないかで受験の合否が大きく変わります。そういった意味では、1つでもミスを減らす工夫が最終的な結果を変える可能性すらあるのです。
まとめ
今回は、大学受験の数学で無双する計算力の身につけ方というテーマで解説をしました。計算力を身に付けていないと、高校数学の演習量をこなしていくのに苦労するだけでなく、解き方が分かっていても受験で間違える可能性があります。
まずは、小学校算数・中学数学の計算を確実にできるようにしましょう。その上で、合格る数学ⅠAⅡBで、計算のテクニックを学ぶことが大事です。なかなか計算のトレーニングに時間を割くのは難しいと思うので、毎日10分でもいいので、少しずつやるのがおススメです。
ある程度、計算テクニックを学んだら、問題演習を通じて、計算のテクニックを使って計算を簡略化出来ないか考えるクセをつけましょう。そういった視点を持って常日頃から計算することが大事になります。受験直前やテスト前には計算ミスノートを作って、自分のミスの傾向を分析して、テスト当日に振り返れるようにしましょう。
こういった積み重ねを重ねることで、大学受験で十分通用するような計算力を身につけることができます。
理系のための大学受験塾SoRaでは、数学が苦手な高校生が多く通っていて、たくさんの方が数学を克服しています。
「実際にどうしたらいいか分からない」
「なんとしても数学を克服したい」
「どうやったら行動に移せるのかを知りたい」
という方はぜひSoRaの無料相談をお申し込みください。あなたの悩みを塾長が直接解決します。
【関連する記事はこちら】