図形問題が苦手な人でも大丈夫!大学受験数学の幾何学的センスの磨き方

数学の図形問題を解いていて、「いや、そんな解き方は思いつかないよ…」と感じたことはありませんか?
「図形問題が得意なあの子は思いつくけど、凡人の私には無理だ」
「図形を見たらパッとひらめくセンスがあればなあ」
と、嘆いたことは誰しも一度はあると思います。
「センス」というと、生まれつきの才能で鍛えられないイメージがあるかもしれません。しかし、地道な作業の積み重ねで、誰でも最低限の幾何学的センスを身につけることができるのです。
確かに、誰もが思いつかないような天才的なひらめきを身につけるのは難しいでしょう。
ですが、大学受験ではそこまでの超人的な能力は求められていません。天才的なひらめきも必要ありません。凡人は凡人なりの戦い方で大学受験を乗り越えることができます。
この記事では、図形問題が苦手な人でも可能な、大学受験で必要となる幾何学的センスの磨き方を紹介します。
【この記事を読むべき人】
- 図形問題が苦手な人
- 図形問題を解くセンスがないと感じている人
- 難関大レベルの図形問題にも対応できるようになりたい人
- 図形問題ができる人の感覚を知りたい人
【自己紹介】
百瀬 浩市
「理系のための大学受験塾SoRa」代表。数学の指導において、幅広いレベルの生徒を担当。定期テストで赤点が続いていた生徒が80点を安定して取れるまでに引き上げる、数学が苦手な難関大学志望者を合格点まで導くといった指導実績を持つ。
幾何学的センスとは何か
この記事では、幾何学的センスを主に以下の3つに分類しています。
- 図形を頭の中でイメージし特徴を捉えて描く能力
- 図形の特徴に気づく能力
- 図の特徴から使うべき定理や公式を割り出す能力
これら3つの能力は下図のようなピラミッド構造になっています。
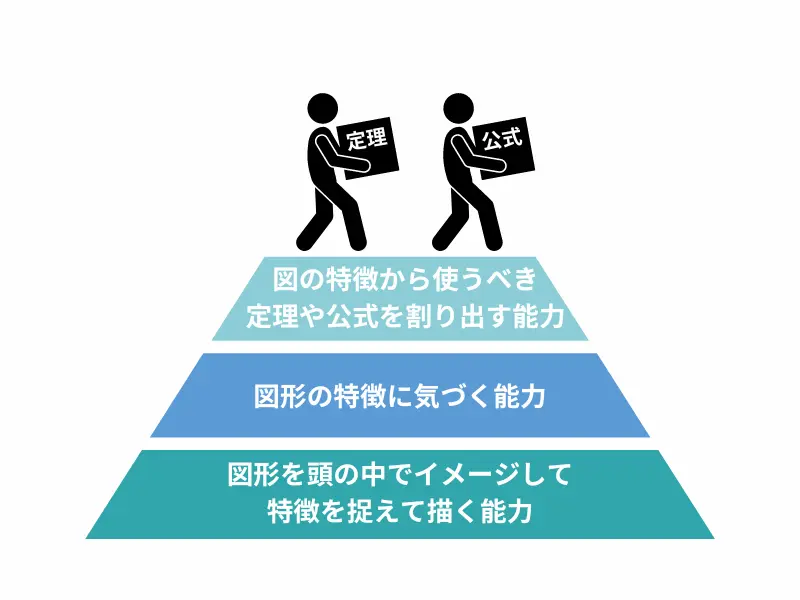
これらは、大学受験の図形問題を解いていく上で、定理や知識を正しく運用していくために必須な能力です。これらの能力がないと、どういった定理や知識が使えるかを判断できないからです。
たとえば、大学受験の図形問題というと、ベクトルや複素数平面といった高校で習う高度な知識を使って解くイメージがあるかもしれません。しかし、実際の入試問題で差がつくポイントは、小学校や中学校で習った基本的な図形の知識を適切に活用できるかどうかにあります。
たとえば、2013年のセンター試験の数ⅠAの試験(私が当時受験生だった年です)の大問3の最初の問題がまさしくそういった問題(下図)でした。
【問題】
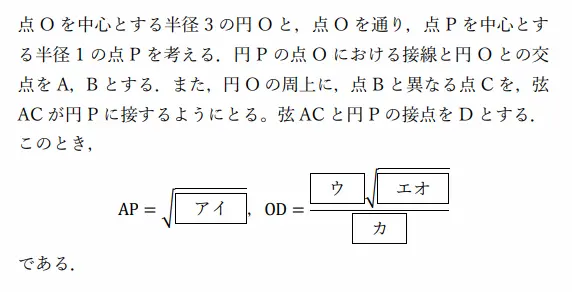
この問題は大問の最初にあたるので、大学入試センター側が正答率9割以上を見込んで作った問題です。
実際、中学で習う二等辺三角形の性質に気づいて面積を利用すれば解ける問題でした。
それにも関わらず、その年のセンター試験の数ⅠAは難化したと評され、そのうち大問3の平均点が異様に低かったのです。
(この年の平均点が51.2点で、前年の平均点が69.9点だったので、19点近く平均点が落ちました)
大問3の最初以外は例年と同じレベル感の問題であったため、大問3の最初の問題を解けずに苦労した受験生が多かったわけです。
実際の解答がこちらです。
【解答】
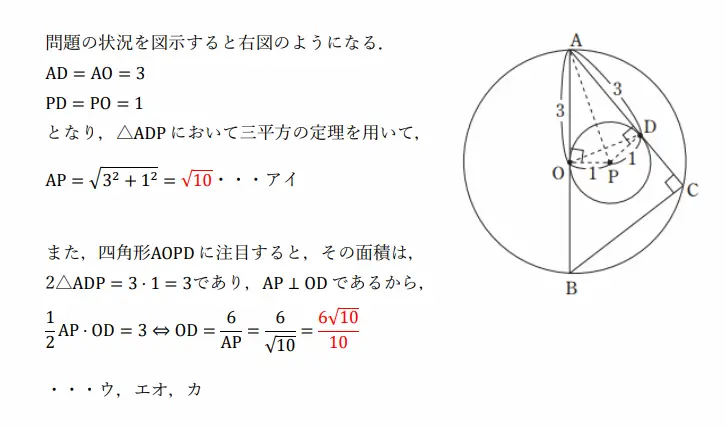
このように見ると、そこまで難しくなさそうですよね。
では、なぜ中学範囲の内容が問われている問題であったにも関わらず、正答率が低かったのか。
それは、多くの受験生が二等辺三角形の特徴に気づかなかったり、描いた図形から面積を比べるという解法のパターンを結び付けられなかったりしたためです。当時の私も最初の問題を見た時に、解法が分からず1分ほど手が止まったのを覚えています。
実は東大をはじめとした難関大からそこまで難易度が高くないような私立大も含めて、毎年こういったことが起こっています。幾何学的センスを磨くことでこういった差がつく図形問題に対応できるようになります。
幾何学的センスの磨き方
その1:問題の図を正確に描く訓練をする
「図形を頭の中でイメージし特徴を捉えて描く能力」は、図形問題を解く上で根幹をなす部分です。その力を鍛えるには、問題で与えられている図をフリーハンドで描き写すのが効果的です(定規やコンパスは使わずに)
問題で与えられている図を描くだけだったら誰でも出来ると思ってしまうかもしれません。しかし、図形問題が極端にできない人は、以下のような点で正しく図を描けていない場合があります。
- 線をまっすぐかけていない
- 角度が正しく書けていない
- 図中の辺の比がおかしい
どういうことか、実際に見てもらった方が早いので、過去に生徒が描いた図の具体例を再現しました。これらを見ていきましょう。
まずは、線をまっすぐかけていない例です(図1)
【図1 線をまっすぐかけていない例】
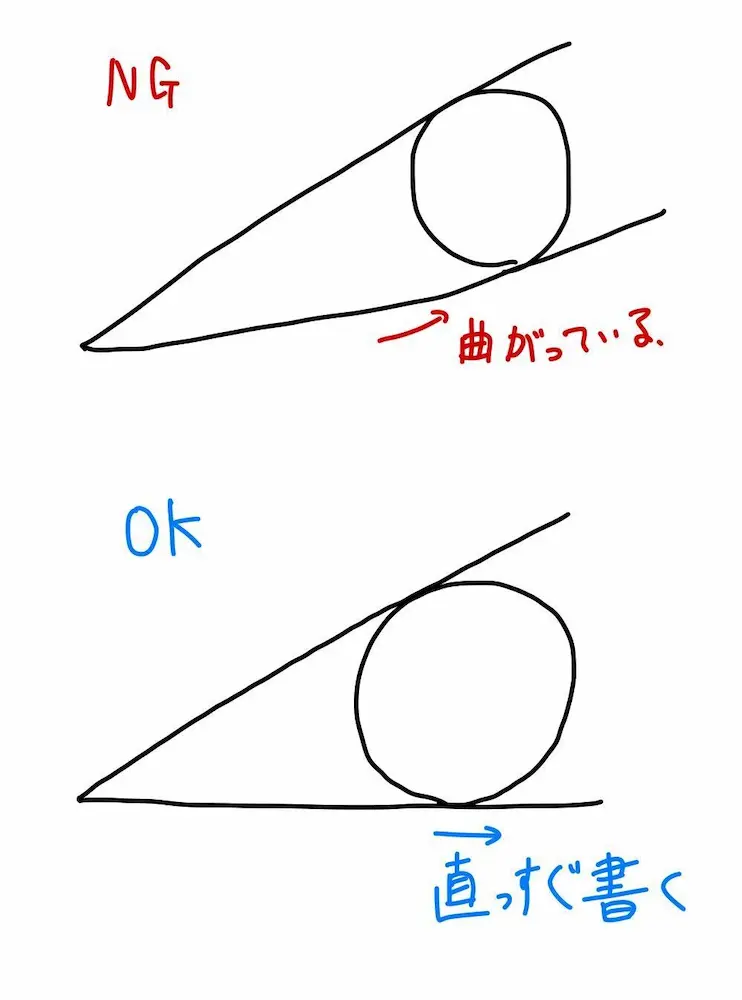
円外の点から円に向かって2本の接線を引いた図なのですが、この図では接線が途中で曲がってしまっています。そのため、2本の線が平行関係のようになってしまっています。
次は、角度が正しく書けていない例です(図2)
【図2 角度が正しく書けていない例】
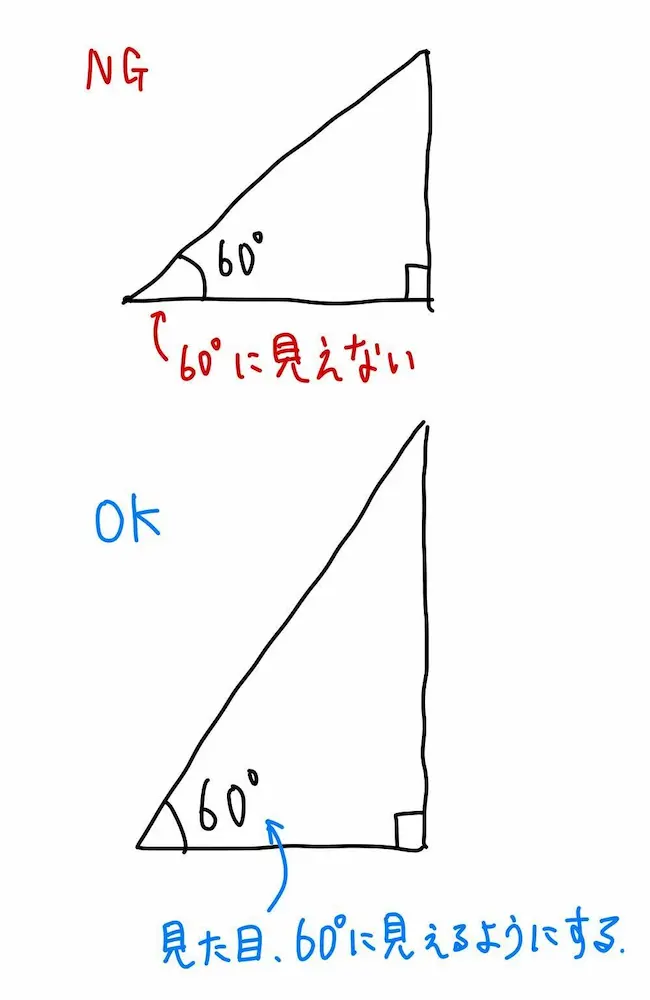
例では60°で描くべき角を45°程度で描いてしまっています。実際の角度と明らかに違う角度を書いてしまうと、問題文の指示に従ってその後の図形を描いたときに大きく乖離してしまい、問題が解けなくなってしまうことがあります。
次は、図中の辺の比がおかしい例です(図3)
【図3 図中の辺の比がおかしい例】
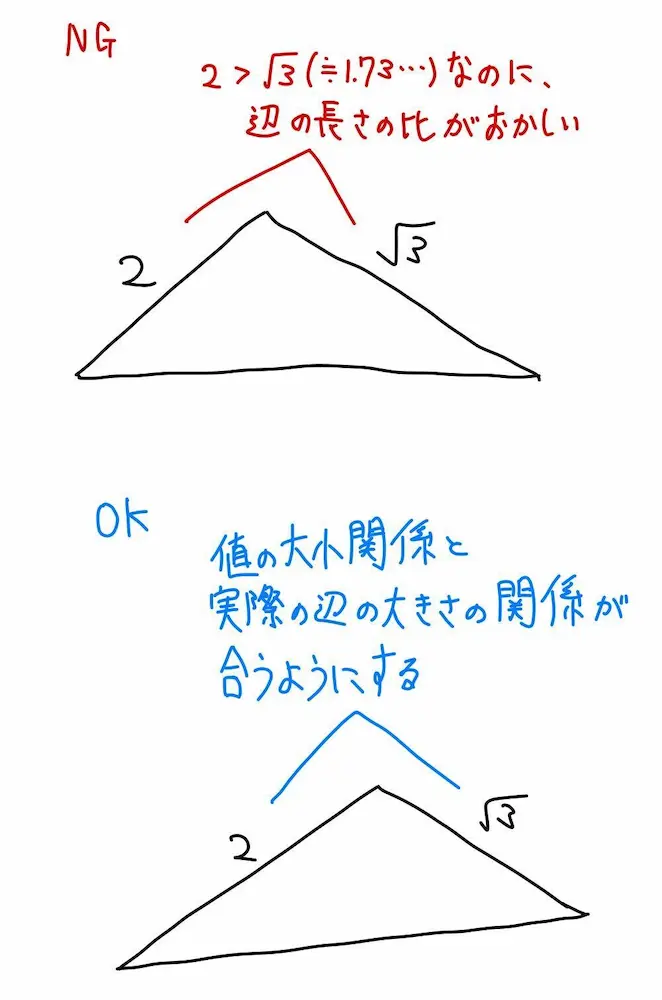
長さ2の辺よりも長さ√3の辺を長く描いてしまっています。実際に、2cmや√3cmを正確に描けていなくても、√3=1.73…という事実から、長さ2よりも若干短いくらいの長さで描くという意識を持つことが重要です。
ここまでを見て、当たり前なことを言っているなと思われたかもしれません。しかし、こういった当たり前のことを丁寧にできるかがカギなのです。最初に、凡人は凡人のやり方でと話しましたが、こういった地道な作業の先に図形問題を解ける力というのはあるのです。
具体的な教材としては、「合格る計算数学ⅠAⅡB」がおススメです。
この参考書には図形の性質に関する基礎的な問題が豊富に掲載されています。この段階では、それらの問題が解ける解けないに関わらず、図をノートに丁寧に写すことを心がけて下さい。
ノートの端に書いたり小さく書いたりしないことがポイントです。ノートを広く使って大きく書くように心がけましょう。図を丁寧に書くという地道な作業から幾何学的センスは磨かれていきます。
その2:問題文から正確に描く訓練をする
先程は描いてある図を同じように描く訓練でした。次は、問題文に書いてある指示通りに図を描く練習です。これもある意味地味な訓練です(笑)
この訓練をすることで、図形の特徴に気づく能力を鍛えることができます。
実際、大学受験では、問題文の中に説明があって、図を自分で書き起こす必要がある問題がよく出てきます。たとえば、以下の立教大学の問題はまさしくそういった問題です。
【問題文】立教大改題

できる人からすると、「ただ説明に従って書くだけじゃない?」と思われるかもしれません。しかし、文章を読んでどういった図になりそうかをイメージし、図の特徴に気づいて書かないといけないので、意外と図を描くのは難しいです。
特に辺の長さや角度の特徴を捉えてその関係性がわかるように書くのは訓練しないとできるようにはなりません。
実際に上記の問題は、以下のような図が書けます。
【正解の図】
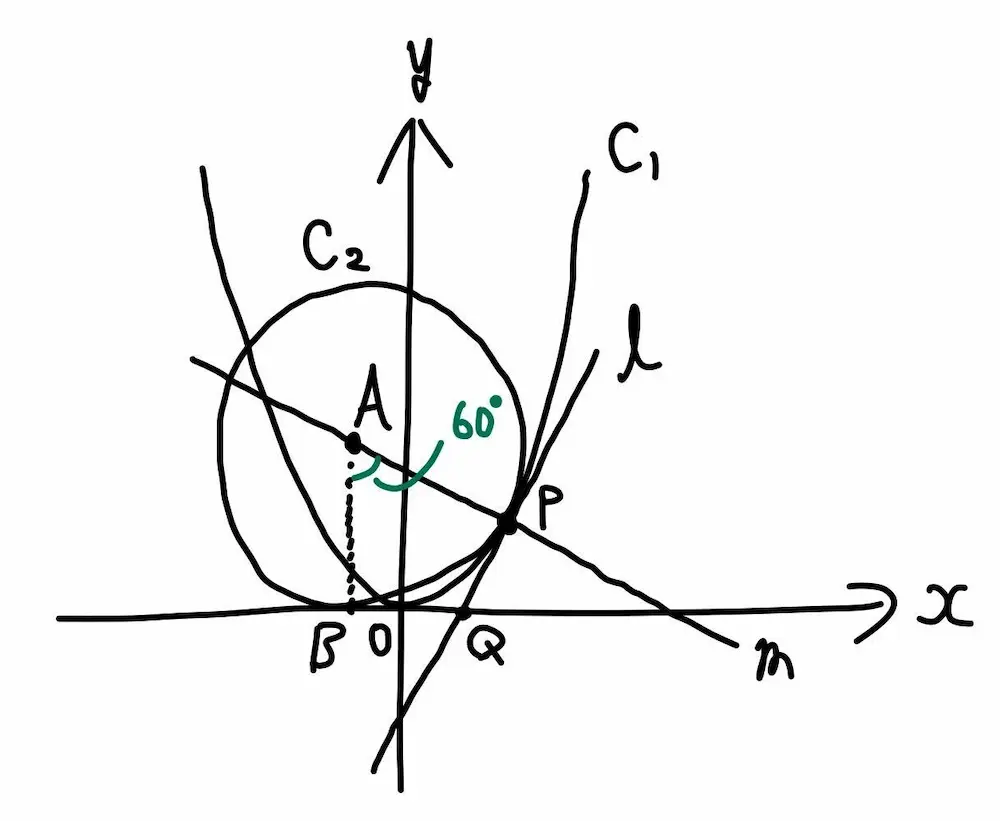
この図のポイントは、直線mが円の接線の法線(垂直をなす直線)であることから、「直線mが円の中心を通ること」に気づかないと描けない図になっています。もしそれに気づかずに書くと以下のような図を描いてしまいます。
【間違っている図】
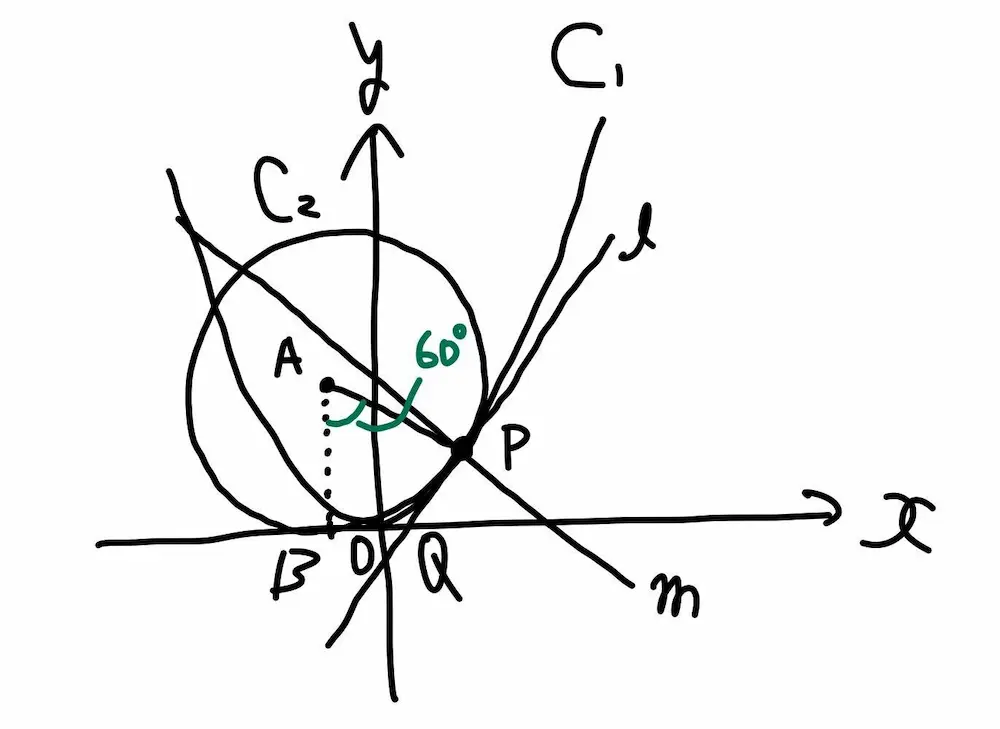
これは実際に生徒が描いた図をそのまま写したものです。実は、このような図を描いた生徒は何人かいました。彼らのうち、「直線mが円の接線の法線(垂直をなす直線)であることから、直線mが円の中心を通ること」ということを知らない人もいましたが、なんと、知っているにも関わらず描けない人もいたのです。
つまり、定理や図形の特徴を知っているだけでなく、それに気づけるようになることが大事なのです。
具体的な鍛え方としては、センター試験の数ⅠAの図形の性質の大問をやりましょう。共通テストではなく、センター試験で構いません。
センター試験の過去問は最初の例で示したように問題文を読み取って図を描く形式の良問が多くあります。問題を解いていきながら文章から図を描く練習をしましょう。
このとき、間違えた問題の答えをただ何となく見るのではなく、
- 図形が正しく描けているか
- 文中から読み取れる以外の情報があったか(あったとしたらその根拠はなにか)
の2点を分析しましょう。
ただ問題を解いていても幾何学的センスは上がっていきません。自分が出来ていなかったところを見つけて、根拠となるものをたどって行けば自然と図形の特徴に気づけるようになります
その3:条件ごとに使える公式や定理を体系化して整理する
先程までは図を描くことにフォーカスをしてきました。ここからは、やっと解くフェーズに入ります。問題を解く上で大事になってくるのは、図の特徴から使うべき定理や公式を割り出す能力です。特に補助線を引くなどして、特定の問題の条件に対してよくやる手法をまとめておきましょう。
たとえば、以下のように、「この条件が来たら○○する!」というのをパターン化しておきたい訳です。
- 60°が出てきたら垂線を引く
- 四角形内で同じ角度が出てきたら円周角を思い浮かべる
- 二等辺三角形が見えたら中線を引く
図形問題を得意とする人が突拍子もなく思いつくようなアイディアは、意外とこのようにパターン化されたものであることが多いです。ある意味、得意な人はこのパターン化されたアイディアを引き出すスピードがめちゃくちゃ速いのです。
苦手な人もそこまで速く見抜けなくても、それらのパターンさえ押さえていれば、解法にたどり着くことはできます。
具体的な鍛え方としては、「教科書だけでは足りない大学入試攻略理系受験生のための図形問題 (河合塾シリーズ)」を使っていくのがおススメです。
教科書だけでは足りない大学入試攻略理系受験生のための図形問題 (河合塾シリーズ)
この参考書では、難関大の過去問やオリジナルの問題に対して、問題条件をどのように解釈して、何を考えるべきかをよりシンプルに伝えてくれています。意識すべきポイントが書かれているため、復習もしやすくなっています。早慶や難関国公立大以上を志望している人にはおススメの一冊です。
使う際の注意点として、どういった図形のときにどういった操作をするのかをノートにまとめるようにしましょう。
たとえば、以下のように「円」を見たときにどういった定理や公式が使えそうなのかを1枚の紙にまとめて、知識を整理しておくと良いです。
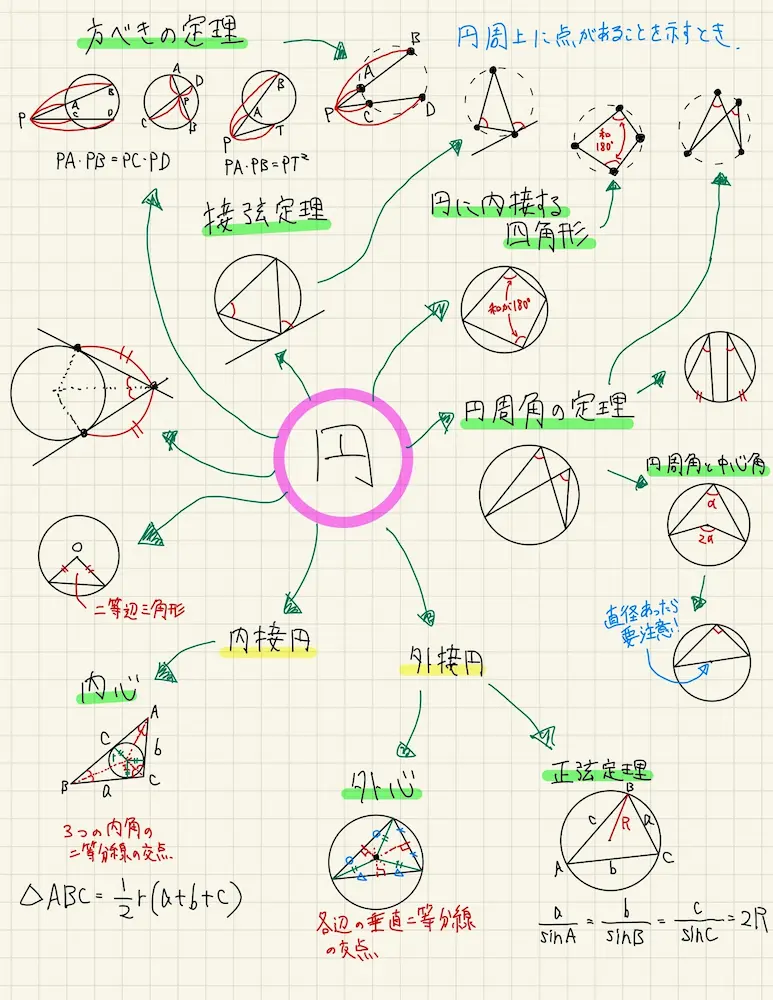
もっと基礎的なレベルからやりたい人は、センター試験の過去問で同様にやってみましょう。いずれにしても問題を解いて復習をする過程で、知識を追加していき、どういうパターンがあるかを自分で体系化していくことが大事です。
まとめ
幾何学的センスを磨くには、以下の3つのことを順にやっていきましょう。
- 図を問題の図を正確に描く訓練をする
- 問題文から正確に描く訓練をする
- 条件ごとに使える公式や定理を体系化して整理する
このように地道な作業ばかりですが、それこそが幾何学的センスの磨き方になります。魔法のようなやり方を期待していた人には申し訳ないですが、これが凡人なりの戦い方なのです。
当塾でも図形問題を苦手にしている生徒さんが多くいらっしゃいますが、例にもれず全員にこの過程を経てもらっています。そして、得意とまではいかないまでも、図形問題に対する苦手意識を払しょくしてくれています。
幾何学的センスはすぐには身につくものではないので、まずは地道な作業から入って少しずつあなたの幾何学的センスを磨いていきましょう。毎日少しずつでも磨き続けることで、大学入試という戦場では大いに役立つはずです。
理系のための大学受験塾SoRaでは、数学が苦手な高校生が多く通っていて、たくさんの方が数学を克服しています。
「実際にどうしたらいいか分からない」
「なんとしても数学を克服したい」
「どうやったら行動に移せるのかを知りたい」
という方はぜひSoRaの無料相談をお申し込みください。あなたの悩みを塾長が直接解決します。
【関連する記事はこちら】
【LINE友だち追加特典】
—❶ 数学やるべき参考書MAP
現在の学力(スタート地点)から志望校(ゴール地点)までをつなぐ、
今やるべき数学の参考書ルートをまとめたMAPです。
・ 学力段階ごとにおすすめの参考書
・ どんなタイプの人に向いているか
・ 使うときに気をつけるポイント
などを具体的に解説しています。
—❷ 週1回配信|公式LINE限定・塾長コラム
公式LINE限定で、週1回の塾長コラムを配信しています。
このコラムでは、
実際に 内部生にその時期お伝えしている内容 をもとに、
高校生・保護者の方それぞれに役立つ情報を発信しています。
・ 学年・時期ごとの正しい過ごし方
・ 成績が伸びる生徒が実践している勉強法
・ 部活動と勉強を両立する考え方
・ 数学の定期テストで効率よく点数を取る方法
など、
少し意識するだけで差がつくポイントを中心にお届けしています。
ご興味のある方は、ぜひ公式LINEにご登録くださいませ。